6. Economic Evaluation of Facility Investments6.1 Project Life Cycle and Economic FeasibilityFacility investment decisions represent major commitments of corporate resources and have serious consequences on the profitability and financial stability of a corporation. In the public sector, such decisions also affect the viability of facility investment programs and the credibility of the agency in charge of the programs. It is important to evaluate facilities rationally with regard to both the economic feasibility of individual projects and the relative net benefits of alternative and mutually exclusive projects. This chapter will present an overview of the decision process for economic evaluation of facilities with regard to the project life cycle. The cycle begins with the initial conception of the project and continues though planning, design, procurement, construction, start-up, operation and maintenance. It ends with the disposal of a facility when it is no longer productive or useful. Four major aspects of economic evaluation will be examined:
It is important to distinguish between the economic evaluation of alternative physical facilities and the evaluation of alternative financing plans for a project. The former refers to the evaluation of the cash flow representing the benefits and costs associated with the acquisition and operation of the facility, and this cash flow over the planning horizon is referred to as the economic cash flow or the operating cash flow. The latter refers to the evaluation of the cash flow representing the incomes and expenditures as a result of adopting a specific financing plan for funding the project, and this cash flow over the planning horizon is referred to as the financial cash flow. In general, economic evaluation and financial evaluation are carried out by different groups in an organization since economic evaluation is related to design, construction, operations and maintenance of the facility while financial evaluations require knowledge of financial assets such as equities, bonds, notes and mortgages. The separation of economic evaluation and financial evaluation does not necessarily mean one should ignore the interaction of different designs and financing requirements over time which may influence the relative desirability of specific design/financing combinations. All such combinations can be duly considered. In practice, however, the division of labor among two groups of specialists generally leads to sequential decisions without adequate communication for analyzing the interaction of various design/financing combinations because of the timing of separate analyses. As long as the significance of the interaction of design/financing combinations is understood, it is convenient first to consider the economic evaluation and financial evaluation separately, and then combine the results of both evaluations to reach a final conclusion. Consequently, this chapter is devoted primarily to the economic evaluation of alternative physical facilities while the effects of a variety of financing mechanisms will be treated in the next chapter. Since the methods of analyzing economic cash flows are equally applicable to the analysis of financial cash flows, the techniques for evaluating financing plans and the combined effects of economic and financial cash flows for project selection are also included in this chapter. Back to top6.2 Basic Concepts of Economic EvaluationA systematic approach for economic evaluation of facilities consists of the following major steps:
It is important to emphasize that many assumptions and policies, some implicit and some explicit, are introduced in economic evaluation by the decision maker. The decision making process will be influenced by the subjective judgment of the management as much as by the result of systematic analysis. The period of time to which the management of a firm or agency wishes to look ahead is referred to as the planning horizon. Since the future is uncertain, the period of time selected is limited by the ability to forecast with some degree of accuracy. For capital investment, the selection of the planning horizon is often influenced by the useful life of facilities, since the disposal of usable assets, once acquired, generally involves suffering financial losses. In economic evaluations, project alternatives are represented by their cash flow profiles over the n years or periods in the planning horizon. Thus, the interest periods are normally assumed to be in years t = 0,1,2, ...,n with t = 0 representing the present time. Let Bt,x be the annual benefit at the end of year t for a investment project x where x = 1, 2, ... refer to projects No. 1, No. 2, etc., respectively. Let Ct,x be the annual cost at the end of year t for the same investment project x. The net annual cash flow is defined as the annual benefit in excess of the annual cost, and is denoted by At,x at the end of year t for an investment project x. Then, for t = 0,1, . . . ,n:
where At,x is positive, negative or zero depends on the values of Bt,x and Ct,x, both of which are defined as positive quantities. Once the management has committed funds to a specific project, it must forego other investment opportunities which might have been undertaken by using the same funds. The opportunity cost reflects the return that can be earned from the best alternative investment opportunity foregone. The foregone opportunities may include not only capital projects but also financial investments or other socially desirable programs. Management should invest in a proposed project only if it will yield a return at least equal to the minimum attractive rate of return (MARR) from foregone opportunities as envisioned by the organization. In general, the MARR specified by the top management in a private firm reflects the opportunity cost of capital of the firm, the market interest rates for lending and borrowing, and the risks associated with investment opportunities. For public projects, the MARR is specified by a government agency, such as the Office of Management and Budget or the Congress of the United States. The public MARR thus specified reflects social and economic welfare considerations, and is referred to as the social rate of discount. Regardless of how the MARR is determined by an organization, the MARR specified for the economic evaluation of investment proposals is critically important in determining whether any investment proposal is worthwhile from the standpoint of the organization. Since the MARR of an organization often cannot be determined accurately, it is advisable to use several values of the MARR to assess the sensitivity of the potential of the project to variations of the MARR value. Back to top6.3 Costs and Benefits of a Constructed FacilityThe basic principle in assessing the economic costs and benefits of new facility investments is to find the aggregate of individual changes in the welfare of all parties affected by the proposed projects. The changes in welfare are generally measured in monetary terms, but there are exceptions, since some effects cannot be measured directly by cash receipts and disbursements. Examples include the value of human lives saved through safety improvements or the cost of environmental degradation. The difficulties in estimating future costs and benefits lie not only in uncertainties and reliability of measurement, but also on the social costs and benefits generated as side effects. Furthermore, proceeds and expenditures related to financial transactions, such as interest and subsidies, must also be considered by private firms and by public agencies. To obtain an accurate estimate of costs in the cash flow profile for the acquisition and operation of a project, it is necessary to specify the resources required to construct and operate the proposed physical facility, given the available technology and operating policy. Typically, each of the labor and material resources required by the facility is multiplied by its price, and the products are then summed to obtain the total costs. Private corporations generally ignore external social costs unless required by law to do so. In the public sector, externalities often must be properly accounted for. An example is the cost of property damage caused by air pollution from a new plant. In any case, the measurement of external costs is extremely difficult and somewhat subjective for lack of a market mechanism to provide even approximate answers to the appropriate value. In the private sector, the benefits derived from a facility investment are often measured by the revenues generated from the operation of the facility. Revenues are estimated by the total of price times quantity purchased. The depreciation allowances and taxes on revenues must be deducted according to the prevailing tax laws. In the public sector, income may also be accrued to a public agency from the operation of the facility. However, several other categories of benefits may also be included in the evaluation of public projects. First, private benefits can be received by users of a facility or service in excess of costs such as user charges or price charged. After all, individuals only use a service or facility if their private benefit exceeds their cost. These private benefits or consumer surplus represent a direct benefit to members of the public. In many public projects, it is difficult, impossible or impractical to charge for services received, so direct revenues equal zero and all user benefits appear as consumers surplus. Examples are a park or roadways for which entrance is free. As a second special category of public benefit, there may be external or secondary beneficiaries of public projects, such as new jobs created and profits to private suppliers. Estimating these secondary benefits is extremely difficult since resources devoted to public projects might simply be displaced from private employment and thus represent no net benefit. Back to top6.4 Interest Rates and the Costs of CapitalConstructed facilities are inherently long-term investments with a deferred pay-off. The cost of capital or MARR depends on the real interest rate (i.e., market interest rate less the inflation rate) over the period of investment. As the cost of capital rises, it becomes less and less attractive to invest in a large facility because of the opportunities foregone over a long period of time. In Figure 6-1, the changes in the cost of capital from 1955 to 1985 are illustrated. This figure presents the market interest rate on a 20-year treasury bond, and the corresponding real interest rate over this period. The real interest rate is calculated as the market interest rate less the general rate of inflation. During the last decade in this figure, the real interest rate has varied substantially, ranging from 10% to -4%. The exceptional nature of the 1980 to 1985 years is dramatically evident: the real rate of interest reached remarkably high historic levels. 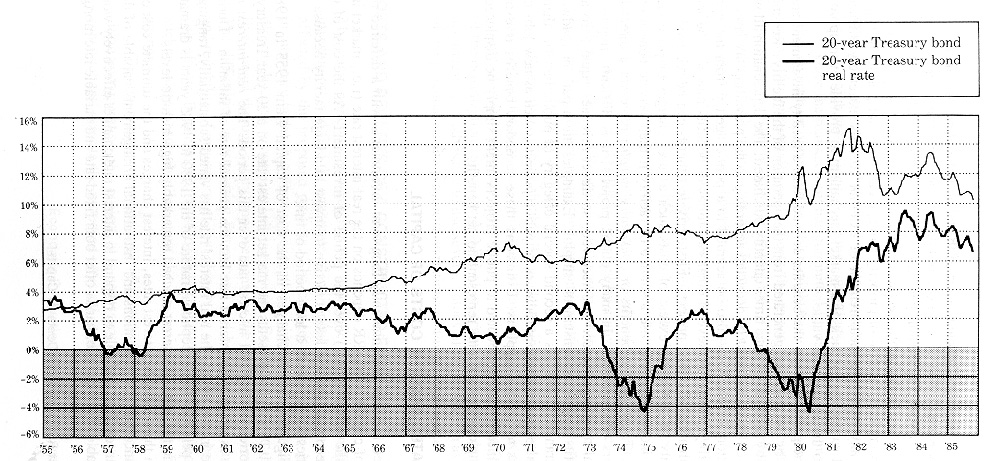
(Reprinted by permission of the Wall Street Journal, ?Dow Jones & Company, Inc. 1985. All rights reserved.) With these volatile interest rates, interest charges and the ultimate cost of projects are uncertain. Organizations and institutional arrangements capable of dealing with this uncertainty and able to respond to interest rate changes effectively would be quite valuable. For example, banks offer both fixed rate and variable rate mortgages. An owner who wants to limit its own risk may choose to take a fixed rate mortgage even though the ultimate interest charges may be higher. On the other hand, an owner who chooses a variable rate mortgage will have to adjust its annual interest charges according to the market interest rates. In economic evaluation, a constant value of MARR over the planning horizon is often used to simplify the calculations. The use of a constant value for MARR is justified on the ground of long-term average of the cost of capital over the period of investment. If the benefits and costs over time are expressed in constant dollars, the constant value for MARR represents the average real interest rate anticipated over the planning horizon; if the benefits and costs over time are expressed in then-current dollars, the constant value for MARR reflects the average market interest rate anticipated over the planning horizon. Back to top6.5 Investment Profit MeasuresA profit measure is defined as an indicator of the desirability of a project from the standpoint of a decision maker. A profit measure may or may not be used as the basis for project selection. Since various profit measures are used by decision makers for different purposes, the advantages and restrictions for using these profit measures should be fully understood. There are several profit measures that are commonly used by decision makers in both private corporations and public agencies. Each of these measures is intended to be an indicator of profit or net benefit for a project under consideration. Some of these measures indicate the size of the profit at a specific point in time; others give the rate of return per period when the capital is in use or when reinvestments of the early profits are also included. If a decision maker understands clearly the meaning of the various profit measures for a given project, there is no reason why one cannot use all of them for the restrictive purposes for which they are appropriate. With the availability of computer based analysis and commercial software, it takes only a few seconds to compute these profit measures. However, it is important to define these measures precisely: 1. Net Future Value and Net Present Value. When an organization makes an investment, the decision maker looks forward to the gain over a planning horizon, against what might be gained if the money were invested elsewhere. A minimum attractive rate of return (MARR) is adopted to reflect this opportunity cost of capital. The MARR is used for compounding the estimated cash flows to the end of the planning horizon, or for discounting the cash flow to the present. The profitability is measured by the net future value (NFV) which is the net return at the end of the planning horizon above what might have been gained by investing elsewhere at the MARR. The net present value (NPV) of the estimated cash flows over the planning horizon is the discounted value of the NFV to the present. A positive NPV for a project indicates the present value of the net gain corresponding to the project cash flows. 2. Equivalent Uniform Annual Net Value. The equivalent uniform annual net value (NUV) is a constant stream of benefits less costs at equally spaced time periods over the intended planning horizon of a project. This value can be calculated as the net present value multiplied by an appropriate "capital recovery factor." It is a measure of the net return of a project on an annualized or amortized basis. The equivalent uniform annual cost (EUAC) can be obtained by multiplying the present value of costs by an appropriate capital recovery factor. The use of EUAC alone presupposes that the discounted benefits of all potential projects over the planning horizon are identical and therefore only the discounted costs of various projects need be considered. Therefore, the EUAC is an indicator of the negative attribute of a project which should be minimized. 3. Benefit Cost Ratio. The benefit-cost ratio (BCR), defined as the ratio of discounted benefits to the discounted costs at the same point in time, is a profitability index based on discounted benefits per unit of discounted costs of a project. It is sometimes referred to as the savings-to-investment ratio (SIR) when the benefits are derived from the reduction of undesirable effects. Its use also requires the choice of a planning horizon and a MARR. Since some savings may be interpreted as a negative cost to be deducted from the denominator or as a positive benefit to be added to the numerator of the ratio, the BCR or SIR is not an absolute numerical measure. However, if the ratio of the present value of benefit to the present value of cost exceeds one, the project is profitable irrespective of different interpretations of such benefits or costs. 4. Internal Rate of Return. The internal rate of return (IRR) is defined as the discount rate which sets the net present value of a series of cash flows over the planning horizon equal to zero. It is used as a profit measure since it has been identified as the "marginal efficiency of capital" or the "rate of return over cost". The IRR gives the return of an investment when the capital is in use as if the investment consists of a single outlay at the beginning and generates a stream of net benefits afterwards. However, the IRR does not take into consideration the reinvestment opportunities related to the timing and intensity of the outlays and returns at the intermediate points over the planning horizon. For cash flows with two or more sign reversals of the cash flows in any period, there may exist multiple values of IRR; in such cases, the multiple values are subject to various interpretations. 5. Adjusted Internal Rate of Return. If the financing and reinvestment policies are incorporated into the evaluation of a project, an adjusted internal rate of return (AIRR) which reflects such policies may be a useful indicator of profitability under restricted circumstances. Because of the complexity of financing and reinvestment policies used by an organization over the life of a project, the AIRR seldom can reflect the reality of actual cash flows. However, it offers an approximate value of the yield on an investment for which two or more sign reversals in the cash flows would result in multiple values of IRR. The adjusted internal rate of return is usually calculated as the internal rate of return on the project cash flow modified so that all costs are discounted to the present and all benefits are compounded to the end of the planning horizon. 6. Return on Investment. When an accountant reports income in each year of a multi-year project, the stream of cash flows must be broken up into annual rates of return for those years. The return on investment (ROI) as used by accountants usually means the accountant's rate of return for each year of the project duration based on the ratio of the income (revenue less depreciation) for each year and the undepreciated asset value (investment) for that same year. Hence, the ROI is different from year to year, with a very low value at the early years and a high value in the later years of the project. 7. Payback Period. The payback period (PBP) refers to the length of time within which the benefits received from an investment can repay the costs incurred during the time in question while ignoring the remaining time periods in the planning horizon. Even the discounted payback period indicating the "capital recovery period" does not reflect the magnitude or direction of the cash flows in the remaining periods. However, if a project is found to be profitable by other measures, the payback period can be used as a secondary measure of the financing requirements for a project. Back to top6.6 Methods of Economic EvaluationThe objective of facility investment in the private sector is generally understood to be profit maximization within a specific time frame. Similarly, the objective in the public sector is the maximization of net social benefit which is analogous to profit maximization in private organizations. Given this objective, a method of economic analysis will be judged by the reliability and ease with which a correct conclusion may be reached in project selection. The basic principle underlying the decision for accepting and selecting investment projects is that if an organization can lend or borrow as much money as it wishes at the MARR, the goal of profit maximization is best served by accepting all independent projects whose net present values based on the specified MARR are nonnegative, or by selecting the project with the maximum nonnegative net present value among a set of mutually exclusive proposals. The net present value criterion reflects this principle and is most straightforward and unambiguous when there is no budget constraint. Various methods of economic evaluation, when properly applied, will produce the same result if the net present value criterion is used as the basis for decision. For convenience of computation, a set of tables for the various compound interest factors is given in Appendix A. Net Present Value MethodLet BPVx be the present value of benefits of a project x and CPVx be the present value of costs of the project x. Then, for MARR = i over a planning horizon of n years,
where the symbol (P|F,i,t) is a discount factor equal to (1+i)-t and reads as follows: "To find the present value P, given the future value F=1, discounted at an annual discount rate i over a period of t years." When the benefit or cost in year t is multiplied by this factor, the present value is obtained. Then, the net present value of the project x is calculated as:
or
If there is no budget constraint, then all independent projects having net present values greater than or equal to zero are acceptable. That is, project x is acceptable as long as
For mutually exclusive proposals (x = 1,2,...,m), a proposal j should be selected if it has the maximum nonnegative net present value among all m proposals, i.e.
provided that NPVj Net Future Value MethodSince the cash flow profile of an investment can be represented by its equivalent value at any specified reference point in time, the net future value (NFVx) of a series of cash flows At,x (for t=0,1,2,...,n) for project x is as good a measure of economic potential as the net present value. Equivalent future values are obtained by multiplying a present value by the compound interest factor (F|P,i,n) which is (1+i)n. Specifically,
Consequently, if NPVx Net Equivalent Uniform Annual Value MethodThe net equivalent uniform annual value (NUVx) refers to a uniform series over a planning horizon of n years whose net present value is that of a series of cash flow At,x (for t= 1,2,...,n) representing project x. That is,
where the symbol (U|P,i,n) is referred to as the capital recovery
factor and reads as follows: "To find the equivalent annual uniform
amount U, given the present value P=1, discounted at an annual discount
rate i over a period of t years." Hence, if NPVx Benefit-Cost Ratio MethodThe benefit-cost ratio method is not as straightforward and unambiguous as the net present value method but, if applied correctly, will produce the same results as the net present value method. While this method is often used in the evaluation of public projects, the results may be misleading if proper care is not exercised in its application to mutually exclusive proposals. The benefit-cost ratio is defined as the ratio of the discounted benefits to the discounted cost at the same point in time. In view of Eqs. (6.4) and (6.6), it follows that the criterion for accepting an independent project on the basis of the benefit-cost ratio is whether or not the benefit-cost ratio is greater than or equal to one:
However, a project with the maximum benefit-cost ratio among a group of mutually exclusive proposals generally does not necessarily lead to the maximum net benefit. Consequently, it is necessary to perform incremental analysis through pairwise comparisons of such proposals in selecting the best in the group. In effect, pairwise comparisons are used to determine if incremental increases in costs between projects yields larger incremental increases in benefits. This approach is not recommended for use in selecting the best among mutually exclusive proposals. Internal Rate of Return MethodThe term internal rate of return method has been used by different analysts to mean somewhat different procedures for economic evaluation. The method is often misunderstood and misused, and its popularity among analysts in the private sector is undeserved even when the method is defined and interpreted in the most favorable light. The method is usually applied by comparing the MARR to the internal rate of return value(s) for a project or a set of projects. A major difficulty in applying the internal rate of return method to economic evaluation is the possible existence of multiple values of IRR when there are two or more changes of sign in the cash flow profile At,x (for t=0,1,2,...,n). When that happens, the method is generally not applicable either in determining the acceptance of independent projects or for selection of the best among a group of mutually exclusive proposals unless a set of well defined decision rules are introduced for incremental analysis. In any case, no advantage is gained by using this method since the procedure is cumbersome even if the method is correctly applied. This method is not recommended for use either in accepting independent projects or in selecting the best among mutually exclusive proposals. Example 6-1: Evaluation of Four Independent Projects The cash flow profiles of four independent projects are shown in Table 6-1. Using a MARR of 20%, determine the acceptability of each of the projects on the basis of the net present value criterion for accepting independent projects.Back to top 6.7 Depreciation and Tax EffectsFor private corporations, the cash flow profile of a project is affected by the amount of taxation. In the context of tax liability, depreciation is the amount allowed as a deduction due to capital expenses in computing taxable income and, hence, income tax in any year. Thus, depreciation results in a reduction in tax liabilities. It is important to differentiate between the estimated useful life used in depreciation computations and the actual useful life of a facility. The former is often an arbitrary length of time, specified in the regulations of the U.S. Internal Revenue Service or a comparable organization. The depreciation allowance is a bookkeeping entry that does not involve an outlay of cash, but represents a systematic allocation of the cost of a physical facility over time. There are various methods of computing depreciation which are acceptable to the U.S. Internal Revenue Service. The different methods of computing depreciation have different effects on the streams of annual depreciation charges, and hence on the stream of taxable income and taxes paid. Let P be the cost of an asset, S its estimated salvage value, and N the estimated useful life (depreciable life) in years. Furthermore, let Dt denote the depreciation amount in year t, Tt denote the accumulated depreciation up to year t, and Bt denote the book value of the asset at the end of year t, where t=1,2,..., or n refers to the particular year under consideration. Then,
The depreciation methods most commonly used to compute Dt and Bt are the straight line method, sum-of-the-years'-digits methods, and the double declining balanced method. The U.S. Internal Revenue Service provides tables of acceptable depreciable schedules using these methods. Under straight line depreciation, the net depreciable value resulting from the cost of the facility less salvage value is allocated uniformly to each year of the estimated useful life. Under the sum-of-the-year's-digits (SOYD) method, the annual depreciation allowance is obtained by multiplying the net depreciable value multiplied by a fraction, which has as its numerator the number of years of remaining useful life and its denominator the sum of all the digits from 1 to n. The annual depreciation allowance under the double declining balance method is obtained by multiplying the book value of the previous year by a constant depreciation rate 2/n. To consider tax effects in project evaluation, the most direct approach is to estimate the after-tax cash flow and then apply an evaluation method such as the net present value method. Since projects are often financed by internal funds representing the overall equity-debt mix of the entire corporation, the deductibility of interest on debt may be considered on a corporate-wide basis. For specific project financing from internal funds, let after-tax cash flow in year t be Yt. Then, for t=0,1,2,...,n,
Besides corporate income taxes, there are other provisions in the federal income tax laws that affect facility investments, such as tax credits for low-income housing. Since the tax laws are revised periodically, the estimation of tax liability in the future can only be approximate. Example 6-2: Effects of Taxes on Investment A company plans to invest $55,000 in a piece of equipment which is expected to produce a uniform annual net revenue before tax of $15,000 over the next five years. The equipment has a salvage value of $5,000 at the end of 5 years and the depreciation allowance is computed on the basis of the straight line depreciation method. The marginal income tax rate for this company is 34%, and there is no expectation of inflation. If the after-tax MARR specified by the company is 8%, determine whether the proposed investment is worthwhile, assuming that the investment will be financed by internal funds. Back to top 6.8 Price Level Changes: Inflation and DeflationIn the economic evaluation of investment proposals, two approaches may be used to reflect the effects of future price level changes due to inflation or deflation. The differences between the two approaches are primarily philosophical and can be succinctly stated as follows:
If these approaches are applied correctly, they will lead to identical results. Let i be the discount rate excluding inflation, i' be the discount rate including inflation, and j be the annual inflation rate. Then,
and
When the inflation rate j is small, these relations can be approximated by
Note that inflation over time has a compounding effect on the price levels in various periods, as discussed in connection with the cost indices in Chapter 5. If At denotes the cash flow in year t expressed in terms of constant (base year) dollars, and A't denotes the cash flow in year t expressed in terms of inflated (then-current) dollars, then
It can be shown that the results from these two equations are identical. Furthermore, the relationship applies to after-tax cash flow as well as to before-tax cash flow by replacing At and A't with Yt and Y't respectively in Equations (6.17) and (6.18). Example 6-3: Effects of Inflation Suppose that, in the previous example, the inflation expectation is 5% per year, and the after-tax MARR specified by the company is 8% excluding inflation. Determine whether the investment is worthwhile.
6.9 Uncertainty and RiskSince future events are always uncertain, all estimates of costs and benefits used in economic evaluation involve a degree of uncertainty. Probabilistic methods are often used in decision analysis to determine expected costs and benefits as well as to assess the degree of risk in particular projects. In estimating benefits and costs, it is common to attempt to obtain the expected or average values of these quantities depending upon the different events which might occur. Statistical techniques such as regression models can be used directly in this regard to provide forecasts of average values. Alternatively, the benefits and costs associated with different events can be estimated and the expected benefits and costs calculated as the sum over all possible events of the resulting benefits and costs multiplied by the probability of occurrence of a particular event:
where q = 1,....,m represents possible events, (Bt|q) and (Ct|q) are benefits and costs respectively in period t due to the occurrence of q, Pr{q} is the probability that q occurs, and E[Bt] and E[Ct] are respectively expected benefit and cost in period t. Hence, the expected net benefit in period t is given by:
For example, the average cost of a facility in an earthquake prone site might be calculated as the sum of the cost of operation under normal conditions (multiplied by the probability of no earthquake) plus the cost of operation after an earthquake (multiplied by the probability of an earthquake). Expected benefits and costs can be used directly in the cash flow calculations described earlier. In formulating objectives, some organizations wish to avoid risk so as to avoid the possibility of losses. In effect, a risk avoiding organization might select a project with lower expected profit or net social benefit as long as it had a lower risk of losses. This preference results in a risk premium or higher desired profit for risky projects. A rough method of representing a risk premium is to make the desired MARR higher for risky projects. Let rf be the risk free market rate of interest as represented by the average rate of return of a safe investment such as U.S. government bonds. However, U.S. government bonds do not protect from inflationary changes or exchange rate fluctuations, but only insure that the principal and interest will be repaid. Let rp be the risk premium reflecting an adjustment of the rate of return for the perceived risk. Then, the risk-adjusted rate of return r is given by:
In using the risk-adjusted rate of return r to compute the net present value of an estimated net cash flow At (t = 0, 1, 2, ..., n) over n years, it is tacitly assumed that the values of At become more uncertain as time goes on. That is:
More directly, a decision maker may be confronted with the subject choice among alternatives with different expected benefits of levels of risk such that at a given period t, the decision maker is willing to exchange an uncertain At with a smaller but certain return atAt where at is less than one. Consider the decision tree in Figure 6-2 in which the decision maker is confronted with a choice between the certain return of atAt and a gamble with possible outcomes (At;)q and respective probabilities Pr{q} for q = 1,2,...,m. Then, the net present value for the series of "certainty equivalents" over n years may be computed on the basis of the risk free rate. Hence:
Note that if rfrp is negligible in comparison with r, then (1 + rf)(1 + rp) = 1 +rf + rp + rfrp = 1 + rHence, for Eq. (6.23) At(1 + r)-t = (atAt/at)(1 + rf)-t(1 + rp)-t =[(atAt)(1 + rf)-t][(1 + rp)-t/at] If at = (1 + rp)-t for t = 1,2,...,n, then Eqs. (6.23) and (6.24) will be identical. Hence, the use of the risk-adjusted rate r for computing NPV has the same effect as accepting at = (1 + rp)-t as a "certainty equivalent" factor in adjusting the estimated cash flow over time. 
Back to top 6.10 Effects of Financing on Project SelectionSelection of the best design and financing plans for capital projects is typically done separately and sequentially. Three approaches to facility investment planning most often adopted by an organization are:
Typically, different individuals or divisions of an organization conduct the analysis for the operating and financing processes. Financing alternatives are sometimes not examined at all since a single mechanism is universally adopted. An example of a single financing plan in the public sector is the use of pay-as-you-go highway trust funds. However, the importance of financial analysis is increasing with the increase of private ownership and private participation in the financing of public projects. The availability of a broad spectrum of new financing instruments has accentuated the needs for better financial analysis in connection with capital investments in both the public and private sectors. While simultaneous assessment of all design and financing alternatives is not always essential, more communication of information between the two evaluation processes would be advantageous in order to avoid the selection of inferior alternatives. There is an ever increasing variety of borrowing mechanisms available. First, the extent to which borrowing is tied to a particular project or asset may be varied. Loans backed by specific, tangible and fungible assets and with restrictions on that asset's use are regarded as less risky. In contrast, specific project finance may be more costly to arrange due to transactions costs than is general corporate or government borrowing. Also, backing by the full good faith and credit of an organization is considered less risky than investments backed by generally immovable assets. Second, the options of fixed versus variable rate borrowing are available. Third, the repayment schedule and time horizon of borrowing may be varied. A detailed discussion of financing of constructed facilities will be deferred until the next chapter. As a general rule, it is advisable to borrow as little as possible when borrowing rates exceed the minimum attractive rate of return. Equity or pay-as-you-go financing may be desirable in this case. It is generally preferable to obtain lower borrowing rates, unless borrowing associated with lower rates requires substantial transaction costs or reduces the flexibility for repayment and refinancing. In the public sector, it may be that increasing taxes or user charges to reduce borrowing involves economic costs in excess of the benefits of reduced borrowing costs of borrowed funds. Furthermore, since cash flow analysis is typically conducted on the basis of constant dollars and loan agreements are made with respect to current dollars, removing the effects of inflation will reduce the cost of borrowing. Finally, deferring investments until pay-as-you-go or equity financing are available may unduly defer the benefits of new investments. It is difficult to conclude unambiguously that one financing mechanism is always superior to others. Consequently, evaluating alternative financing mechanisms is an important component of the investment analysis procedure. One possible approach to simultaneously considering design and financing alternatives is to consider each combination of design and financing options as a specific, mutually exclusive alternative. The cash flow of this combined alternative would be the sum of the economic or operating cash flow (assuming equity financing) and the financial cash flow over the planning horizon. Back to top6.11 Combined Effects of Operating and Financing Cash FlowsA general approach for obtaining the combined effects of operating and financing cash flows of a project is to make use of the additive property of net present values by calculating an adjusted net present value. The adjusted net present value (APV) is the sum of the net present value (NPV) of the operating cash flow plus the net present value of the financial cash flow due to borrowing or raising capital (FPV). Thus,
where each function is evaluated at i=MARR if both the operating and the financing cash flows have the same degree of risk or if the risks are taken care of in other ways such as by the use of certainty equivalents. Then, project selection involving both design and financing alternatives is accomplished by selecting the combination which has the highest positive adjusted present value. The use of this adjusted net present value method will result in the same selection as an evaluation based on the net present value obtained from the combined cash flow of each alternative combination directly. To be specific, let At be the net operating cash flow,
Similarly, let
The tax shields for interest on borrowing (for t = 1, 2, ..., n) are usually given by
where It is the interest paid in year t and Xt is the marginal corporate income tax rate in year t. In view of Eqs. (6.13), (6.27) and (6.28), we obtain
When MARR = i is applied to both the operating and the financial cash flows in Eqs. (6.13) and (6.28), respectively, in computing the net present values, the combined effect will be the same as the net present value obtained by applying MARR = i to the combined cash flow in Eq. (6.29). In many instances, a risk premium related to the specified type of operation is added to the MARR for discounting the operating cash flow. On the other hand, the MARR for discounting the financial cash flow for borrowing is often regarded as relatively risk-free because debtors or holders of corporate bonds must be paid first before stockholders in case financial difficulties are encountered by a corporation. Then, the adjusted net present value is given by
where NPV is discounted at r and FPV is obtained from the rf rate. Note that the net present value of the financial cash flow includes not only tax shields for interest on loans and other forms of government subsidy, but also on transactions costs such as those for legal and financial services associated with issuing new bonds or stocks. The evaluation of combined alternatives based on the adjusted net present value method should also be performed in dollar amounts which either consistently include or remove the effects of inflation. The MARR value used would reflect the inclusion or exclusion of inflation accordingly. Furthermore, it is preferable to use after-tax cash flows in the evaluation of projects for private firms since different designs and financing alternatives are likely to have quite different implications for tax liabilities and tax shields. In theory, the corporate finance process does not necessarily require a different approach than that of the APV method discussed above. Rather than considering single projects in isolation, groups or sets of projects along with financing alternatives can be evaluated. The evaluation process would be to select that group of operating and financing plans which has the highest total APV. Unfortunately, the number of possible combinations to evaluate can become very large even though many combinations can be rapidly eliminated in practice because they are clearly inferior. More commonly, heuristic approaches are developed such as choosing projects with the highest benefit/cost ratio within a particular budget or financial constraint. These heuristic schemes will often involve the separation of the financing and design alternative evaluation. The typical result is design-driven or finance-driven planning in which one or the other process is conducted first. Example 6-4: Combined Effects of Operating and Financing Plans A public agency plans to construct a facility and is considering two design alternatives with different capacities. The operating net cash flows for both alternatives over a planning horizon of 5 years are shown in Table 6-4. For each design alternative, the project can be financed either through overdraft on bank credit or by issuing bonds spanning over the 5-year period, and the cash flow for each financing alternative is also shown in Table 6-4. The public agency has specified a MARR of 10% for discounting the operating and financing cash flows for this project. Determine the best combination of design and financing plan ifBack to top(a) a design is selected before financing plans are considered, orThe net present values (NPV) of all cash flows can be computed by Eq.(6.5), and the results are given at the bottom of Table 6-4. The adjusted net present value (APV) combining the operating cash flow of each design and an appropriate financing is obtained according to Eq. (6.25), and the results are also tabulated at the bottom of Table 6-4. 6.12 Public versus Private Ownership of FacilitiesIn recent years, various organizational ownership schemes have been proposed to raise the level of investment in constructed facilities. For example, independent authorities are assuming responsibility for some water and sewer systems, while private entrepreneurs are taking over the ownership of public buildings such as stadiums and convention centers in joint ventures with local governments. Such ownership arrangements not only can generate the capital for new facilities, but also will influence the management of the construction and operation of these facilities. In this section, we shall review some of these implications. A particular organizational arrangement or financial scheme is not necessarily superior to all others in each case. Even for similar facilities, these arrangements and schemes may differ from place to place or over time. For example, U.S. water supply systems are owned and operated both by relatively large and small organizations in either the private or public sector. Modern portfolio theory suggest that there may be advantages in using a variety of financial schemes to spread risks. Similarly, small or large organizations may have different relative advantages with respect to personnel training, innovation or other activities. Differences in Required Rates of ReturnA basic difference between public and private ownership of facilities is that private organizations are motivated by the expectation of profits in making capital investments. Consequently, private firms have a higher minimum attractive rate of return (MARR) on investments than do public agencies. The MARR represents the desired return or profit for making capital investments. Furthermore, private firms often must pay a higher interest rate for borrowing than public agencies because of the tax exempt or otherwise subsidized bonds available to public agencies. International loans also offer subsidized interest rates to qualified agencies or projects in many cases. With higher required rates of return, we expect that private firms will require greater receipts than would a public agency to make a particular investment desirable. In addition to different minimum attractive rates of return, there is also an important distinction between public and private organizations with respect to their evaluation of investment benefits. For private firms, the returns and benefits to cover costs and provide profit are monetary revenues. In contrast, public agencies often consider total social benefits in evaluating projects. Total social benefits include monetary user payments plus users' surplus (e.g., the value received less costs incurred by users), external benefits (e.g., benefits to local businesses or property owners) and nonquantifiable factors (e.g., psychological support, unemployment relief, etc.). Generally, total social benefits will exceed monetary revenues. While these different valuations of benefits may lead to radically different results with respect to the extent of benefits associated with an investment, they do not necessarily require public agencies to undertake such investments directly. First, many public enterprises must fund their investments and operating expenses from user fees. Most public utilities fall into this category, and the importance of user fee financing is increasing for many civil works such as waterways. With user fee financing, the required returns for the public and private firms to undertake the aforementioned investment are, in fact, limited to monetary revenues. As a second point, it is always possible for a public agency to contract with a private firm to undertake a particular project. All other things being equal, we expect that private firms will require larger returns from a particular investment than would a public agency. From the users or taxpayers point of view, this implies that total payments would be higher to private firms for identical services. However, there are a number of mitigating factors to counterbalance this disadvantage for private firms. Tax Implications of Public Versus Private OrganizationsAnother difference between public and private facility owners is in their relative liability for taxes. Public entities are often exempt from taxes of various kinds, whereas private facility owners incur a variety of income, property and excise taxes. However, these private tax liabilities can be offset, at least in part, by tax deductions of various kinds. For private firms, income taxes represent a significant cost of operation. However, taxable income is based on the gross revenues less all expenses and allowable deductions as permitted by the prevalent tax laws and regulations. The most significant allowable deductions are depreciation and interest. By selecting the method of depreciation and the financing plan which are most favorable, a firm can exert a certain degree of control on its taxable income and, thus, its income tax. Another form of relief in tax liability is the tax credit which allows a direct deduction for income tax purposes of a small percentage of the value of certain newly acquired assets. Although the provisions for investment tax credit for physical facilities and equipment had been introduced at different times in the US federal tax code, they were eliminated in the 1986 Tax Reformation Act except a tax credit for low-income housing. Of course, a firm must have profits to take direct advantage of such tax shields, i.e., tax deductions only reduce tax liabilities if before-tax profits exist. In many cases, investments in constructed facilities have net outlays or losses in the early years of construction. Generally, these losses in early years can be offset against profits occurred elsewhere or later in time. Without such offsetting profits, losses can be carried forward by the firm or merged with other firms' profits, but these mechanisms will not be reviewed here. Effects of Financing PlansMajor investments in constructed facilities typically rely upon borrowed funds for a large portion of the required capital investments. For private organizations, these borrowed funds can be useful for leverage to achieve a higher return on the organizations' own capital investment. For public organizations, borrowing costs which are larger than the MARR results in increased "cost" and higher required receipts. Incurring these costs may be essential if the investment funds are not otherwise available: capital funds must come from somewhere. But it is not unusual for the borrowing rate to exceed the MARR for public organizations. In this case, reducing the amount of borrowing lowers costs, whereas increasing borrowing lowers costs whenever the MARR is greater than the borrowing rate. Although private organizations generally require a higher rate of return than do public bodies (so that the required receipts to make the investment desirable are higher for the private organization than for the public body), consideration of tax shields and introduction of a suitable financing plan may reduce this difference. The relative levels of the MARR for each group and their borrowing rates are critical in this calculation. Effects of Capital Grant SubsidiesAn important element in public investments is the availability of capital grant subsidies from higher levels of government. For example, interstate highway construction is eligible for federal capital grants for up to 90% of the cost. Other programs have different matching amounts, with 50/50 matching grants currently available for wastewater treatment plants and various categories of traffic systems improvement in the U.S. These capital grants are usually made available solely for public bodies and for designated purposes. While the availability of capital grant subsidies reduces the local cost of projects, the timing of investment can also be affected. In particular, public subsidies may be delayed or spread over a longer time period because of limited funds. To the extent that (discounted) benefits exceed costs for particular benefits, these funding delays can be costly. Consequently, private financing and investment may be a desirable alternative, even if some subsidy funds are available. Implications for Design and ConstructionDifferent perspectives and financial considerations also may have implications for design and construction choices. For example, an important class of design decisions arises relative to the trade-off between capital and operating costs. It is often the case that initial investment or construction costs can be reduced, but at the expense of a higher operating costs or more frequent and extensive rehabilitation or repair expenditures. It is this trade-off which has led to the consideration of "life cycle costs" of alternative designs. The financial schemes reviewed earlier can profoundly effect such evaluations. For financial reasons, it would often be advantageous for a public body to select a more capital intensive alternative which would receive a larger capital subsidy and, thereby, reduce the project's local costs. In effect, the capital grant subsidy would distort the trade-off between capital and operating costs in favor of more capital intensive projects. The various tax and financing considerations will also affect the relative merits of relatively capital intensive projects. For example, as the borrowing rate increases, more capital intensive alternatives become less attractive. Tax provisions such as the investment tax credit or accelerated depreciation are intended to stimulate investment and thereby make more capital intensive projects relatively more desirable. In contrast, a higher minimum attractive rate of return tends to make more capital intensive projects less attractive. Back to top6.13 Economic Evaluation of Different Forms of OwnershipWhile it is difficult to conclude definitely that one or another organizational or financial arrangement is always superior, different organizations have systematic implications for the ways in which constructed facilities are financed, designed and constructed. Moreover, the selection of alternative investments for constructed facilities is likely to be affected by the type and scope of the decision-making organization. As an example of the perspectives of public and private organizations, consider the potential investment on a constructed facility with a projected useful life of n years. Let t = 0 be the beginning of the planning horizon and t = 1, 2, ... n denote the end of each of the subsequent years. Furthermore, let Co be the cost of acquiring the facility at t = 0, and Ct be the cost of operation in year t. Then, the net receipts At in year t is given by At = Bt - Ct in which Bt is the benefit in year t and At may be positive or negative for t = 0, 1, 2, ..., n. Let the minimum attractive rate of return (MARR) for the owner of the facility be denoted by i. Then, the net present value (NPV) of a project as represented by the net cash flow discounted to the present time is given by
Then, a project is acceptable if NPV
Thus, the minimum uniform annual gross receipt B which makes the project economically acceptable can be determined from Equation (6.32), once the acquisition and operation costs Ct of the facility are known and the MARR is specified. Example 6-5: Different MARRs for Public and Private Organizations For the facility cost stream of a potential investment with n = 7 in Table 6-5, the required uniform annual gross receipts B are different for public and private ownerships since these two types of organizations usually choose different values of MARR. With a given value of MARR = i in each case, the value of B can be obtained from Eq. (6.32). With a MARR of 10%, a public agency requires at least B = $184,000. By contrast, a private firm using a 20% MARR before tax while neglecting other effects such as depreciation and tax deduction would require at least B = $219,000. Then, according to Eq. (6.31), the gross receipt streams for both public and private ownerships in Table 6-5 will satisfy the condition NPV = 0 when each of them is netted from the cost stream and discounted at the appropriate value of MARR, i.e., 10% for a public agency and 20% (before tax) for a private firm. Thus, this case suggests that public provision of the facility has lower user costs. Example 6-6: Effects of Depreciation and Tax Shields for Private Firms Using the same data as in Example 6-5, we now consider the effects of depreciation and tax deduction for private firms. Suppose that the marginal tax rate of the firm is 34% in each year of operation, and losses can always be offset by company-wide profits. Suppose further that the salvage value of the facility is zero at the end of seven years so that the entire amount of cost can be depreciated by means of the sum-of-the-years'-digits (SOYD) method. Thus, for the sum of digits 1 through 7 equal to 28, the depreciation allowances for years 1 to 7 are respectively 7/28, 6/28, ..., 1/28 of the total depreciable value of $ 500,000, and the results are recorded in column 3 of Table 6-6. For a uniform annual gross receipt B = $219,000, the net receipt before tax in Column 6 of Table 6-5 in Example 6-5 can be used as the starting point for computing the after-tax cash flow according to Equation (6.13) which is carried out step-by-step in Table 6-6. (Dollar amounts are given to the nearest $1,000). By trial and error, it is found that an after-tax MARR = 14.5% will produce a zero value for the net present value of the discounted after-tax flow at t = 0. In other words, the required uniform annual gross receipt for this project at 14.5% MARR after tax is also B = $219,000. It means that the MARR of this private firm must specify a 20% MARR before tax in order to receive the equivalent of 14.5% MARR after tax.
Example 6-7: Effects of Borrowing on Public Agencies Suppose that the gross uniform annual receipt for public ownership is B = $190,000 instead of $184,000 for the facility with cost stream given in Column 2 of Table 6-5. Suppose further that the public agency must borrow $400,000 (80% of the facility cost) at 12% annual interest, resulting in an annual uniform payment of $88,000 for the subsequent seven years. This information has been summarized in Table 6-7. The use of borrowed funds to finance a facility is referred to as debt financing or leveraged financing, and the combined cash flow resulting from operating and financial cash flows is referred to as the levered cash flow.
Example 6-8: Effects of Leverage and Tax Shields for Private Organizations Suppose that the uniform annual gross receipt for a private firm is also B = $190,000 (the same as that for the public agency in Example 6-7). The salvage value of the facility is zero at the end of seven years so that the entire amount of cost can be depreciated by means of the sum-of-the-years'-digit (SOYD) method. The marginal tax rate of the firm is 34% in each year of operation, and losses can always be offset by company-wide profits. Suppose further that the firm must borrow $400,000 (80% of the facility cost) at a 12% annual interest, resulting in an annual uniform payment of $88,000 for the subsequent seven years. The interest charge each year can be computed as 12% of the remaining balance of the loan in the previous year, and the interest charge is deductible from the tax liability.
Example 6-9: Comparison of Public and Private Ownership. In each of the analyses in Examples 6-5 through 6-8, a minimum required uniform annual gross receipt B is computed for each given condition whether the owner is a public agency or a private firm. By finding the value of B which will lead to NPV = 0 for the specified MARR for the organization in each case, various organizational effects with or without borrowing can be analyzed. The results are summarized in Table 6-9 for comparison. In this example, public ownership with a 80% loan and a 10% MARR has the same required benefit as private ownership with an identical 80% loan and a 14.5% after-tax MARR.
Back to top 6.14 References
6.15 Problems
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|